[ACM/算法]01背包问题详解+扩展

Posted on | Edited on | In | Comments:

01背包问题作为著名的动态规划问题之一，在算法学习中的意义不言而喻。

最近刷到一道题，在01背包问题中有稍微改变。

BeiBaoQuestion

题中不仅要求输出最大概率之和，还要求输出楼盘ID。

动态规划问题

例如输入序列为：

5 10
2 0.2
3 0.3
4 0.44
5 0.55
6 0.6

贪心算法：

第一种解法是贪心算法

  1. 将所有楼盘序列计算出单位概率。
  2. 按照单位概率将序列排序。
  3. 依次从高概率遍历到低概率，从而得到局部最优解。

算法代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def greedy():
    number, fund = input().split(' ')
    fund = int(fund)
    array = []
    max_prob = []
    max_value = 0
    for i in range(int(number)):  # 输入锁定金额和概率
        value, prob = input().split(' ')
        current_id = i+1
        array.append([current_id, int(value), float(prob), float(prob)/float(value)])
    print(array)
    # 第四位排序
    array.sort(key=take_four, reverse=True)
    print(array)
    for i in array:  # 选中最佳可能的资金
        max_value += i[1]
        if max_value < fund:
            max_prob.append([i[0], i[2]])
    print('max_prob:', max_prob)
    max_prob_value = 0
    for i in max_prob:
        max_prob_value = i[1] + max_prob_value
    print(max_prob_value, [x[0] for x in max_prob])

我们可以得到结果

0.99 [4, 3]

显然这不是我们想要的结果，因为最优解应该为1，2，4 = 1.05才对。

动态规划

寻找最大概率值

使用动态规划的方法解决该问题需要对问题建立转移方程：

  1. 输入楼盘数量为number，总资金为fund

  2. 输入楼盘的数据raw_data.

  3. 定义子问题P(i, v)为在前i个楼盘中挑选总价值不超过v的楼盘，并且每个楼盘只能选择一次，使得最终抽中的总概率最大。我们此时的最优解记作max_prob(i, w)，其中1<=i<=number,1<=w<=fund。

  4. 当我们考虑第i个楼盘的时候：

    如果不选择，则总资金容量不变，改为问题P(i-1, w)

    如果选择这个楼盘，则总资金剩余容量变小，改问题为P(i-1, w-wi)

  5. 最优解的问题就是比较3中两个方案哪一个是最佳的：

    max_prob(i,w) = max{max_prob(i-1,w),max_prob(i-1,w-wi)+valuei}

例如输入序列为：

5 10
2 0.2
3 0.3
4 0.44
5 0.55
6 0.6

假设我们一共有10W金钱，楼盘价值分别为2，3，4，5，6。楼盘概率分别为0.2，0.3，0.44，0.55，0.6。

那么我们通过转移方程可以推算出以下表格max_prob：

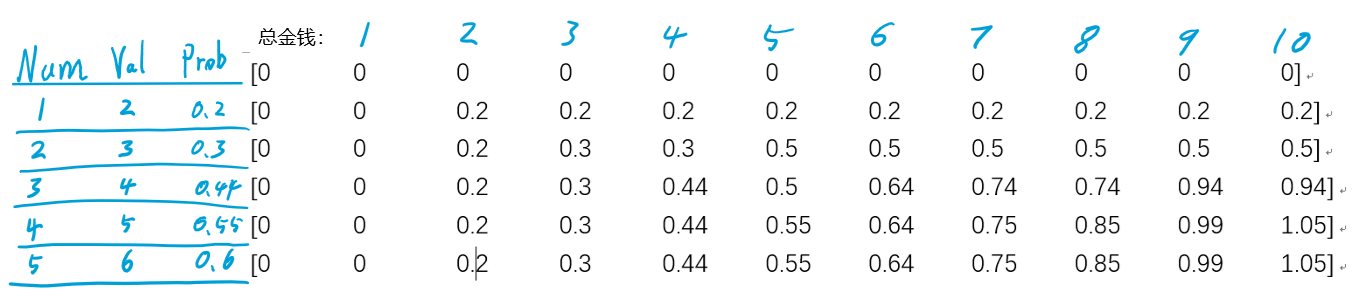
1552028354656

推算过程:

  1. 建立一个表格，大小为number×fund。

  2. 逐层遍历，按列遍历。

    1. 当资金为1的时候，没有任何房产可以购买。

    2. 当资金为2的时候，可以购买房产1。

    3. 当资金为3的时候，可以购买房产1，但是当遍历到（2，3）的时候，对比

      max{max_prob(i-1,w),max_prob(i-1,w-wi)+valuei}

      其中max_prob(i-1,w) 代表i-1行w列。

      其中max_prob(i-1,w)为0.2，max_prob(i-1,w-wi)+valuei 为0.2-0.2 + 0.3 = 0.3

    4. 经过逐次的遍历，得到最终整个矩阵数据。

算法代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def dynasty():
    # ----------------输入数据----------------------
    number, fund = input().split(' ')
    fund = int(fund)
    number = int(number)
    max_prob = [[0 for col in range(fund+1)] for row in range(number+1)]
    raw_data = []
    for i in range(int(number)):  # 输入锁定金额和概率
        value, prob = input().split(' ')
        current_id = i+1
        raw_data.append([current_id, int(value), float(prob), float(prob)/float(value)])
    # ---------------计算概率分布矩阵-------------------
    all_max = 0
    for i in range(1, number+1):  # 遍历所有的房价,number为房产个数
        for j in range(1, fund+1):  # 遍历所有总金额,
            # print(i, j, raw_data[i-1][1])
            if j < raw_data[i-1][1]:  # 假定的总金额小于当前房产的价格
                max_prob[i][j] = max_prob[i-1][j]  # 概率等于之前的
            else:
                max_prob[i][j] = max(max_prob[i-1][j], (max_prob[i-1][j-raw_data[i-1][1]] + raw_data[i-1][2]))
                if max_prob[i][j] > all_max:  # 记录概率最大值
                    all_max = max_prob[i][j]
   
	# ----------------打印概率分布矩阵---------------
    print('概率分布矩阵:\n', max_prob)
    print('all_max_prob:', all_max)
计算楼盘的序列

  1. 定义指针（i,j）倒序遍历表格

  2. 从末尾开始遍历,寻找按顺序排列第一次出现all_max节点,将all_max修改为all_max-raw_data[i][prob]

  3. 当找到第一个星号1.05后移动指针位置到（i-1,j-1）,检测当前值是否为第一次出现的all_max,如果是，标记为星，并重复2步骤，直到遍历到（0，0）

  4. 输出所有标记星所在的行即为楼盘序列。

    1552030438642

算法代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# ----------------从表中推出楼盘列表--------------
id_list = []
# id_list.append(max_id)
# 反向查找关键节点
j = fund  # 定义列位置
i = number  # 定义行位置
while i != 0 and j != 0:  # 从max_prob表右下位置开始，逆序遍历
    # print('all_max:', all_max)
    print('当前遍历的节点i,j,prob:', i, j, max_prob[i][j])
    # print('value:', int(max_prob[i][j]))
    # print('value_(i,j-1):', int(max_prob[i][j-1]))
    # 如果同行上一列的的概率值仍然为最大，则切换到上一列
    if max_prob[i][j-1] == all_max:
        # print('j = j-1')
        j = j-1
    # 如果同列上一行的的概率值仍然为最大，则切换到上一行
    elif max_prob[i - 1][j] == all_max:
        # print('i = i-1')
        i = i-1
    # 处于拐点，可能是一个关键点。
    else:
        # print('test', int(max_prob[i][j]), int(all_max - raw_data[i-1][2]))
        # 如果当前概率等于最大的概率，则是关键点
        if max_prob[i][j] == all_max:
            id_list.append(raw_data[i-1][0])  # 保存当前楼盘的id
            all_max = all_max - raw_data[i-1][2]  # 转换当前最大概率，寻找下一个关键节点
            print('----当前楼盘是关键点之一：', i, '下一个节点prob为：', all_max)
        i = i-1
        j = j-1
print(id_list)

算法源码点击 这里

引用：

https://blog.csdn.net/huanghaocs/article/details/77920358

https://zhuanlan.zhihu.com/p/30959069